问题的提出

给定一个整数n，求出能用来匹配所有被n整除的二进制数的正则表达式(任意一个即可)

例如：

  • n = 1, regex = (0|1)*
  • n = 4, regex = (0|1)*00

分析

对于n为2^k的情况，由二进制数的表达方式可知，对应的正则表达式为(0|1)*0{k}

不难理解，每次二进制数左移一位，对应的值变为原来的两倍。

那么对于更一般的情况（n != 2^k）时，该怎么做呢？

一开始考虑通解会比较困难，那不如用一个具体存在的数字来作为例子——考虑n=7的情况。

在这种情况下，我们可以把所有的数字，按照与7的模的结果，分为7类，用State(0)代表当前的数能被7整除，用State(1)代表当前的数被7整除余数为1……

我们来查看一个简单状态的转移：

  • State = 0,
    • 如果下一个数字是1， 转移到状态 (0 * 2 + 1) mod 7 = 1
    • 如果下一个数字是0， 转移到状态(0 * 2) mod 7 = 0

显然我们可以总结出如下规律：

  • State = k,
    • 如果下一个数字是1， 转移到状态(k * 2 + 1) mod 7
    • 如果下一个数字是0， 转移到状态(k * 2) mod 7

易知，对于n=7, 有 2n = 14个转移线路和n = 7个状态

如果把它用图画出来，大概就是类似下面的这个样子:

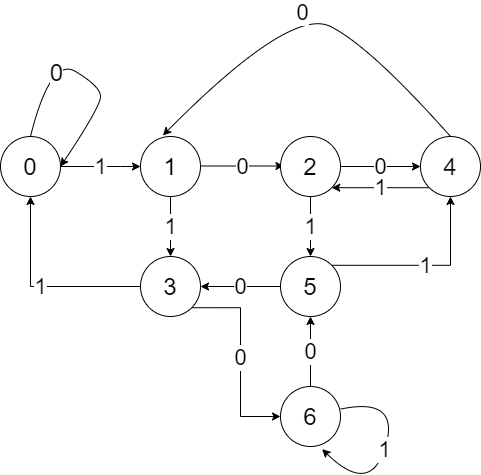
这是一个有限状态自动机（deterministic finite automaton, DFA），那么现在问题就被转换成如何由DFA求其等价的正则表达式了。

这篇博客介绍了几个消除状态的方法

  • 归纳法，参见《自动机理论、语言和计算导论 第二版》
  • 消结消弧法
  • Arden’s Lemma 解方程（高斯消元）

以下采用的是归纳法+消除节点的方法来做。

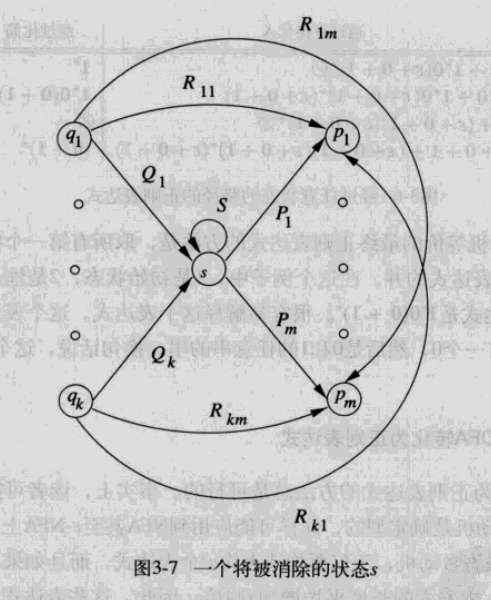
当消除状态s时，自动机中所有经过s的状态都不存在了
可以把与s相关的状态划分成三类

  1. 假设 q1,q2,…,qn是s的前驱状态,记作集合Q

  2. p1, p2, …, pm 是s的后继状态，记作集合P

  3. S是从s到s的环

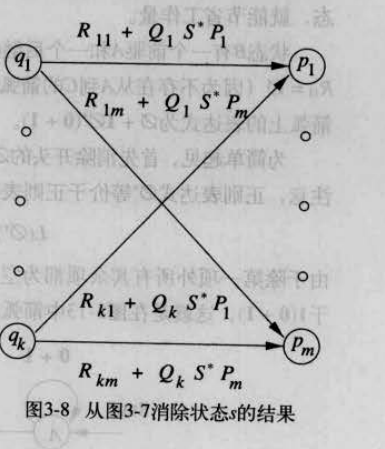
当删除状态s时删除了所有涉及状态s的边，作为补偿，需要给p_i,q_j集合中引入

新的正则表达式 {q_j}S*{p_i}

新边 Arc(q_j, p_i, {q_j}S*{p_i})
该正则表达式需要与状态q_j -> p_i 上原有的表达式r_ij合并（如果没有，就设原来的表达式为空集)

这样说也许有点费解，结合图片也许更能理解

以下图片来源于《自动机理论、语言和计算导论 第二版》第三章（Introduction to Automata Theory, Languages, and Computation）

代码实现

想了下还是删掉了

如果你能找到的话，代码就在gist上，只有聪明的 人才能看到……