The Observer Pattern

观察者模式（有时又被称为发布/订阅模式）是软件设计模式的一种。在此种模式中，一个目标对象管理所有相依于它的观察者对象，并且在它本身的状态改变时主动发出通知。这通常透过呼叫各观察者所提供的方法来实现。此种模式通常被用来实现事件处理系统。

一个简单的观察者模式的实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
trait Publisher {
  private var subscribers: Set[Subscriber] = Set()
  
  def subscribe(subscriber: Subscriber): Unit = {
    subscribers += subscriber
  }
  
  def unsubscribe(subscriber: Subscriber): Unit = {
    subscribers -= subscriber
  }
  
  def publish(): Unit = {
    subscribers.foreach(_.handler(this))
  }
}

trait Subscriber {
  def handler(pub: Publisher): Unit
}

我们可以用观察者模式重写之前的银行账户的问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class BankAccount extends Publisher {
  private var balance = 0
  def currentBalance: Int = balance

  def deposit(amount: Int): Unit = {
    if (amount > 0) {
      balance += amount
      publish()
    }
  }

  def withdraw(amount: Int): Unit = {
    if (0 < amount && amount <= balance) {
      balance -= amount
    } else throw new Error("insufficient funds")
  }
}


class Consolidator(observed: List[BankAccount]) extends Subscriber {
  observed.foreach(_.subscribe(this))
  private var total: Int = 0

  compute()
  private def compute(): Unit = {
    total = observed.map(_.currentBalance).sum
  }

  def handler(pub: Publisher): Unit = compute()


  def totalBalance: Int = total
  
}

我们可以简单测试下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
scala> val a = new BankAccount()
val a: BankAccount = BankAccount@170f0fd6

scala> val b = new BankAccount()
val b: BankAccount = BankAccount@673fdc28

scala> val c = new Consolidator(List(a,b))
val c: Consolidator = Consolidator@22f1a340

scala> c.totalBalance
val res5: Int = 0

scala> a.deposit(20)

scala> c.totalBalance
val res7: Int = 20

scala> b.deposit(30)

scala> c.totalBalance
val res9: Int = 50

观察者模式有好处有坏处，一个明显的优点是，它把状态和视图进行了解耦，我们可以在原有的代码上方便地添加新的观察者。

另外一个问题是，当我们绑定过多观察者后，并发就成了问题。

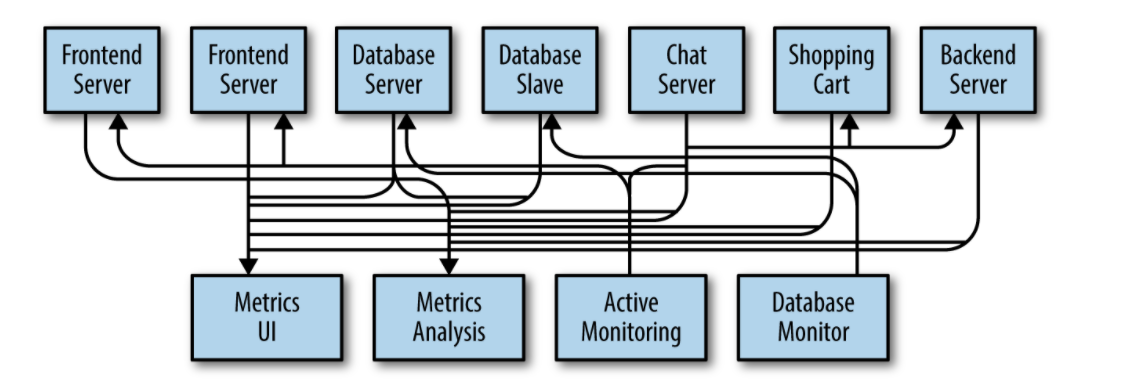
其实解决方法已经有了，想一下消息队列(如Kafka的实现)

⬆图片来自《Kafka 权威指南》

Functional Reactive Programming

FRP(Functional Reactive Progarmming)其实不是什么新鲜玩意(就像Lambda一样)，1997就有人提出过

框架方面的话，有

Flapjax

Elm

Bacon.js

React4J

（有些已经凉凉了）

下面介绍的FRP不是基于以上框架，而是自己实现的最简单的class——frp.signal，下一小节将详细介绍这个模块。

什么是FRP呢

Functional reactive programming (FRP) is a programming paradigm for reactive programming (asynchronous dataflow programming) using the building blocks of functional programming (e.g. map, reduce, filter). FRP has been used for programming graphical user interfaces (GUIs), robotics, games, and music, aiming to simplify these problems by explicitly modeling time.

简单来说就是把时间作为参数，用f(time)来对事件序列建模

下面以鼠标移动举例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 维护随时间变动的信号
// 这个函数返回当前的鼠标位置
mousePosition()


// 判断当前的位置是否在矩形内，并给出对应的信号量
def inRectangle(lowerLeft: Position, uperRight: Position): Signal[Boolean] = 
  Signal {
    val pos = mousePosition()
    lowerLeft <= pos && pos <= uperRight
  }

// 常量信号可以这样定义
val sig = Signal(3)

// 随时间变化的信号量可以这样定义
// `Signal`本身的实现是不可变的，只有`Var`的子类提供的`update`接口可以更改对应的值
val sig = Var(3)
sig.update(5)

Scala有一个语法糖f(E1,..,En) = E等价于f.update(E1,...,En, E)

当n=0也成立，所以

sig.update(5)等价于sig() = 5

上面为什么要多此一举的实现可变呢？这是因为

  • 我们可以在信号间使用map变换，能在时间轴上，自动地帮我们维护两个信号量之间地关系
  • 普通地变量则不然，我们需要手动地维护状态更新

考虑有两个信号量a,b

1
2
a = 2
b = 2 * a

当a = a + 1时为了维护b = 2 * a的关系，需要手动更新一遍

如果用上面的方法呢？

1
2
3
a() = 2
b() = 2 * a()
a() = 3

这种情况下a()的更新能直接被反应到b()上

这样讲还是过于抽象，我们回到之前银行账户的例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class BankAccount {
  private val balacne = Var(0)
  def deposit(amount: Int): Unit = {
    if (amount > 0) {
      val b = balacne() // 如果不这样做会出现循环依赖，想一想为什么
      balacne() = b + amount
    }
  }
  
  def withdraw(amount: Int): Unit = {
    if (0 < amount && amount <= balance()) {
      val b = balance()
      balance() = b - amount
    } else throw new Error("insufficient funds")
  }
 
}

object accounts {
  def consolidator(accts: List[BankAccount]): Signal[Int] = {
    Signal(accts.map(_.balance()).sum)
  }
  
  val a = new BankAccount()
  val b = new BankAccount()
  
  val c = consolidator(List(a, b))
  c() // 0
  a deposit 20
  c() // 20
  b deposit 30
  c() // 50
  
  // 定义一个新的变化率信号量
  val xchange = Signal(246.00)
  val inDollar = Signal(c() * xchange())
  inDollar() // 12300.00
  b withdraw 10
  inDollar() // 984.00
}

和使用观察者模式的代码相比，这个代码更简洁，因为把复杂度封装到了Singal库里面

本小节有一个简单的练习

1
2
3
4
5
6
7
val num = Var(1)
val twice = Signal(num() * 2)
num() = 2

var num = Var(1)
val twice = Signal(num() * 2)
num = Var(2)

这两个twice得到的值相同吗？

显然不同。

这里之所以会造成不同，是因为，下面的num = Var(2)语句

这里新定义的信号量和之前的信号量完全没有关系了

如下图

1
2
3
4
5
6
           |--------------2  <----  num
           |   
----------1|

--------------------------2  <----  twice

而对于上面的语句，num()=2等价于num.update(2)

1
2
3
4
5
6
7
           |--------------2  <----  num
           |   
----------1|

----------2|  
           |
           |--------------4  <----  twice

A FRP Implementation

上一小节说的frp.singal，这一节给出具体的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Signal[T](expr: => T) {
  def apply(): T = ???
}

object Signal {
  def apply[T](expr: => T) = new Singal(expr)
}

class Var[T](expr: => T) extends Signal[T](expr) {
  def update(expr: => T): Unit = ???
}

object Var {
  def apply[T](expr: => T) = new Var(expr)
}

每一个信号需要维护以下几个变量

  • 当前的值
  • 当前用来定义的表达式
  • 观察者集合——其他的信号量依赖于此信号量的值

我们如何来记录观察者的变换呢？

  • 当信号量的表达式发生改变时，要知道有哪些signals的值受这个变更的影响或定义
  • 如果我们已经知道了上述收到影响的信号量有哪些，那么当执行sig()函数时，意味着对所有当前信号的观察者发送了一次变更的请求
  • 当sig的值变化时，所有之前观察这个信号的观察者集合的所有信号，都会被重新计算，并且sig.observers的值会被清空
  • 在所有观察者信号量重新计算的过程中，只要调用者还是依赖sig的值，那么在重算过程中会把自己依次加入sig.observers集合内

那么如何实现呢？一个最简单的办法是维护一个全局的类似于栈的数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class StackableVariable[T](init: T) {
  private var values: List[T] = List(init)
  def value: T  = values.head
  def withValue[R](newValue: T)(op: => R): R = {
    values = newValue :: values
    try op finally values = values.tail
  }
}

object NoSignal extends StackableVariable[Nothing](???) {  }

object Signal {
  // Signal[_] 表示能够接受任何一个Signal类型的数据
  private val caller = new StackableVariable[Signal[_]](NoSignal)
  def apply[T](expr: => T) = new Signal(expr)
}

准备工作完成后，现在来看下具体的Signal类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Signal[T](expr: => T) {
  import Signal._
  private var myExpr: () => T = _
  private var myValue: T = _
  private var observers: Set[Signal[_]] = Set()
  update(expr)
  
  protected def update(expr: => T): Unit = {
    myExpr = () => expr
    computValue()
  }
  
  protected def computValue(): Unit = {
    myValue = caller.withValue(this)(myExpr())
  }
  
  def apply() = {
    observers += caller.value
    // 避免循环引用
    assert(!caller.value.observers.contain(this), "cylic signal definition")
    myValue
  }
}

上面的代码已经把基本的框架给搭起来了，但是还缺少了调用方信号的重新计算

singal会改变，当

  • 对Var类型的变量，调用update函数
  • 这个值依赖的其他信号发生了变更

需要对computeValue函数简单修改下

1
2
3
4
5
6
7
8
9
protected def computValue(): Unit = {
  val newValue = caller.withValue(this)(myExpr())
  if (newValue != myValue) {
    myValue = newValue
    val obs = observers
    observers = Set()
    obs.foreach(_.computeValue())
  }
}

同时把上面NoSignal的函数补全

1
2
3
object NoSignal extends Signal[Nothing](???) {
  override def computeValue() = ()
}

剩下的是信号的recall

1
2
3
4
5
6
7
8
9
10
class Var[T](expr: => T) extends Signal[T](expr) {
  // override 是为了去除 protected 修饰符，使得非子类的外部实例也能更新对应值
  override def update(expr: => T): Unit = {
    super.update(expr)
  }
}

object Var {
  def apply[T](expr: => T) = new Var(expr)
}

现在再来回顾之前的部分，我们用一个全局变量来保存状态

1
private val caller = new StackableVariable[Signal[_]](NoSignal)

这条语句在多线程的情况下是有竞态(race condiction)风险的

为了修改成线程安全(thread safe)的，需要稍微改动

  • 加锁——简单粗暴，但是会影响执行速度，并且有死锁风险
  • 使用 thread-local 的状态，每一个进程单独维护一个拷贝的变量，Scala提供的支持是scala.util.DynamicVariable

将上面的代码修改下

1
2
3
4
object  Signal {
  private val caller = new DynamicVariable[Signal[_]](NoSignal)
  ...
}

thread-local也不是完美的

  • 需要查询JVM的全局哈希表，影响性能
  • 当线程被多个任务使用时会存在性能问题

Calculator

模拟推文

你也许知道，某404网站的消息长度是有限制的，每一条推文的长度不能超过140个字符

当用户在输入时，如果能及时显示还有多少个字符剩余，看起来会更加方便

传统的方法是在文本框设置一个onChange的事件回调函数

这里我们用函数式的方式来实现（如前文所述，使用的是Signal）

首先我们要实现的是TweetLength.scala的函数tweetRemainingCharsCount

1
2
3
4

def tweetRemainingCharsCount(tweetText: Signal[String]): Signal[Int] = {
  Signal(MaxTweetLength - tweetLength(tweetText()))
}

这里复用了tweetLength函数，统计长度的时候是按照code point而不是文本的长度直接计算的

计算长度完整的spec可以参考推特的文档

这个项目的前端使用的框架是scala.js

首先需要在sbt里编译(IDE不支持这个操作)

1
sbt:progfun2-calculator> webUI/fastOptJS

编译完成后，可以使用浏览器打开网页web-ui/index.html，查看效果

这一部分对应的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// TWEET LENGTH

def setupTweetMeasurer(): Unit = {
  val tweetText = textAreaValueSignal("tweettext")
  val remainingCharsArea =
    document.getElementById("tweetremainingchars").asInstanceOf[html.Span]

  val remainingCount = TweetLength.tweetRemainingCharsCount(tweetText)
  Signal {
    remainingCharsArea.textContent = remainingCount().toString
  }

  val color = TweetLength.colorForRemainingCharsCount(remainingCount)
  Signal {
    remainingCharsArea.style.color = color()
  }
}

说实话，之前没用过scala.js，不是很懂咋编译成js了

接下来是给剩余的字数标上颜色

  • 如果还有15或更多的字符可以输入，标为绿色
  • 如果剩余可输入的字符数，小于15，大于等于0，标记为橙色
  • 如果已经超出了限制的字符数，标为红色
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 // 我第一次写的时候写错了
def colorForRemainingCharsCount(remainingCharsCount: Signal[Int]): Signal[String] = {
    val remainCount = remainingCharsCount()
    Signal(
      if (remainCount >= 15) "green"
      else if (remainCount >= 0) "orange"
      else "red")
  }


  def colorForRemainingCharsCount(remainingCharsCount: Signal[Int]): Signal[String] = {
    Signal {
      val cnt = remainingCharsCount()
      if (cnt >= 15) "green"
      else if (cnt >= 0) "orange"
      else "red"
    }
  }

重新编译后即可查看效果(话说有没有自动重编的功能，这样每次都要重新编译也太麻烦了)

解二次方程

二次方程的解法，经典的例子就是判别式法

1
Δ = b² - 4ac

对应的两个解为

1
(-b ± √Δ) / 2a

需要实现的代码，一个简单的版本如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
object Polynomial extends PolynomialInterface {
  def computeDelta(a: Signal[Double], b: Signal[Double],
      c: Signal[Double]): Signal[Double] = {
    Signal(
      b() * b() - 4 * a() * c()
    )
  }

  def computeSolutions(a: Signal[Double], b: Signal[Double],
      c: Signal[Double], delta: Signal[Double]): Signal[Set[Double]] = {
    Signal(
      if (delta() < 0) Set()
      else {
        Set(
          (-b() + math.sqrt(delta())) / (2*a()),
          (-b() - math.sqrt(delta())) / (2*a())
        )
      }
    )
  }
}

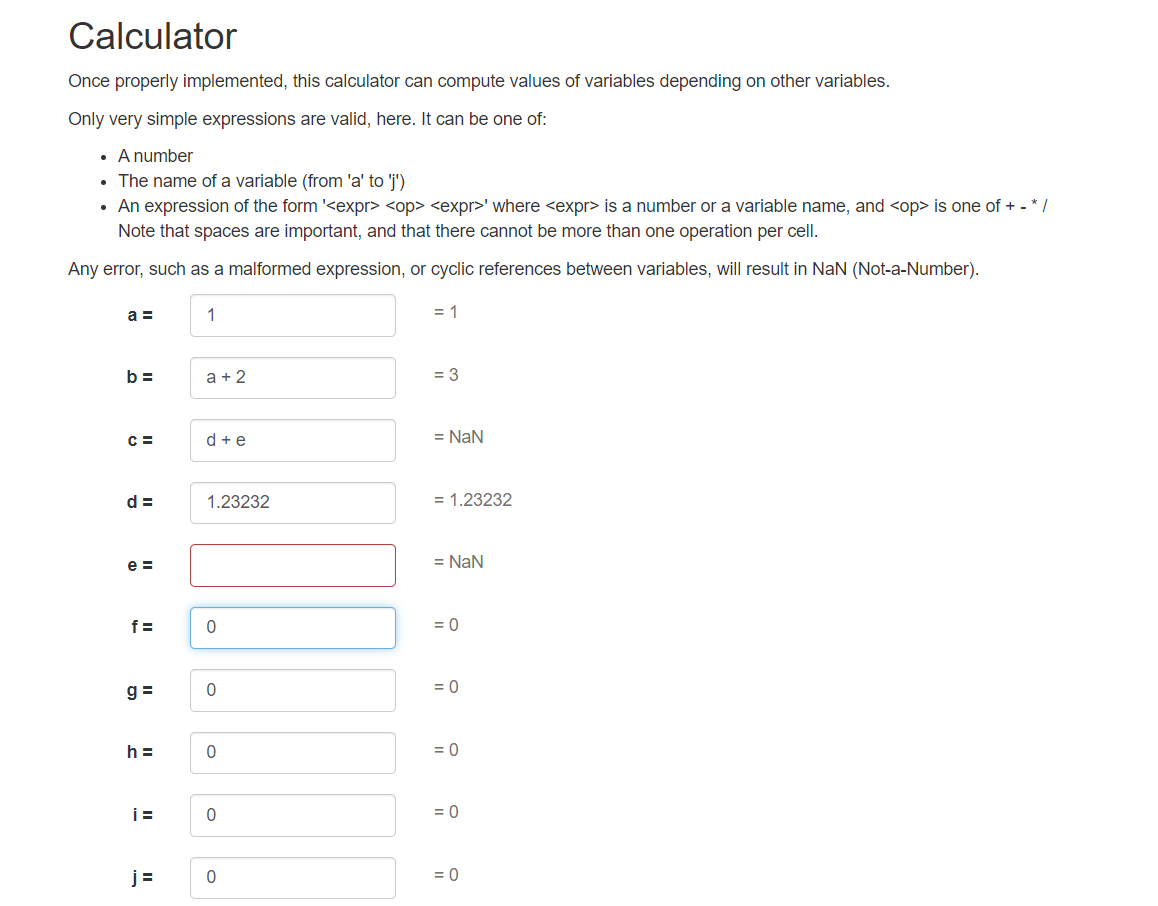
计算器

有了之前两问的基础，看下最后的问题

考虑我们有若干个变量，每个变量可以依赖之前的变量来求值

对于存在循环依赖和未定义变量的表达式，需要输出NaN

补全如下的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
package calculator

sealed abstract class Expr
final case class Literal(v: Double) extends Expr
final case class Ref(name: String) extends Expr
final case class Plus(a: Expr, b: Expr) extends Expr
final case class Minus(a: Expr, b: Expr) extends Expr
final case class Times(a: Expr, b: Expr) extends Expr
final case class Divide(a: Expr, b: Expr) extends Expr

object Calculator extends CalculatorInterface {
  def computeValues(
      namedExpressions: Map[String, Signal[Expr]]): Map[String, Signal[Double]] = {
    ???
  }

  def eval(expr: Expr, references: Map[String, Signal[Expr]]): Double = {
    ???
  }

  /** Get the Expr for a referenced variables.
   *  If the variable is not known, returns a literal NaN.
   */
  private def getReferenceExpr(name: String,
      references: Map[String, Signal[Expr]]) = {
    references.get(name).fold[Expr] {
      Literal(Double.NaN)
    } { exprSignal =>
      exprSignal()
    }
  }
}

一个简单的实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def computeValues(
  namedExpressions: Map[String, Signal[Expr]]): Map[String, Signal[Double]] = {
  for {
    (variable, expression) <- namedExpressions
  } yield {variable -> Signal(eval(expression(), namedExpressions))}
}

def eval(expr: Expr, references: Map[String, Signal[Expr]]): Double = {
  expr match {
    case Literal(v) => v
    case Ref(r) =>
      val ref = getReferenceExpr(r, references)
      eval(ref, references - r)
    case Plus(a, b) => eval(a, references) + eval(b, references)
    case Minus(a, b)  => eval(a, references) - eval(b, references)
    case Times(a, b)  => eval(a, references) * eval(b, references)
    case Divide(a, b) => eval(a, references) / eval(b, references)
  }
}

至此，这门课程也完结了。