本文的写作灵感来自与凤凰木的面试题 《我们为什么要考斐波那契数列──一道上机笔试题的解析，兼谈技术面试与编程基本功》,先行致谢。

UPDATE:2024-04 上面这篇文章已经有了更新的版本 凤凰木的笔记:面试中的斐波那契数列问题

同时，也是填之前的坑

要求计算斐波那契数列的第50 * 10 ^6 项，前四位和后四位连起来就是本次的key

这个有空专门写个文章讲讲fib的计算套路吧

前置知识

  • 了解基本的大学数学知识(数列，等比公式，待定系数法，矩阵…)
  • 基本的编程知识
  • 了解简单的Scala语法(非必须)

问题的引出

斐波那契数列（The Fibonacci sequence， OEIS A000045 ）的定义如下：

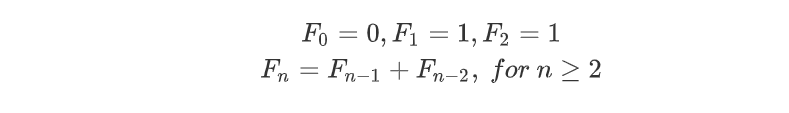
很多问题都和Fibonacci数列有关

  • 奥数题：爬楼梯，铺砖块
  • 欧几里得算法求最大公约数时，最坏情况为两个连续的 Fibonacci 数列
  • 斐波那契回调线，在金融交易市场中被用做确认支撑位和阻力位的一种工具

一道简单的小学数学题

现在有长度为10， 宽度为2的长方形地板需要铺设地砖，地砖有两种

  • 一种是长度为1，宽度为2的
  • 一种是长度为2，宽度为1的

试问不同的铺设方案有多少种？

比如长度为3，宽度为2的地板铺设方案，有3种可选的铺设方案

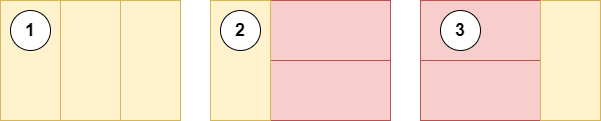
这就是一个典型的求斐波那契数列的问题，和爬楼梯类似。

设f(n)为长度为n，宽度为2的长方形地盘的铺设方案数，对于较小规模的情况，穷举可得方案数

f(1) = 1, f(2) = 2, f(3) = 3

对于长度为n的地板，需要求f(n)，分类考虑下面两种情况

  • 最右边的地砖是竖着放的，剩下需要摆放的长度减少至n-1，那么这个问题可以被化归成f(n-1)
  • 最右边的地砖是横着放的，那么这个地砖下面的一个位置必然也是横着放的，这两个地砖一共占用了2的长度，剩下需要拜访的长度减少至n-2, 那么这个问题可以被化归成f(n-2)

综合考虑以上两种情况(已经列举完了)，长度为n的方案数=长度为n-1的方案数+长度为n-2的方案数

所以有状态转移方程 f(n) = f(n-1) + f(n-2)

如果你耐着性子手算，结果应该是这样的

1
2
3
4
5
6
7
8
9
10
f(1)=1
f(2)=2
f(3)=3
f(4)=5
f(5)=8
f(6)=13
f(7)=21
f(8)=34
f(9)=55
f(10)=89

据此可以写出代码如下

1
2
3
4
5
6
7
8
9
def fib(n: Int): Int = {
  var (a, b) = (0, 1)
  for (i <- 1 to n) {
    val temp = b
    b = a + b
    a = temp
  }
  b
}

一点简单的扩展

上面的代码，能不能一行搞定？

1
def fib (n: Int): Int = if (n <= 1) n else fib(n-1) + fib(n-2)

乍一看很优美，但仔细考虑下，好像有点不对劲

如果在2020年的低配笔记本上运行的话，到40左右就会感觉明显的卡顿

这个问题在大学C语言教材里4.3.2 斐波那契序列（计算与时间）也有提到，下面是书中的图

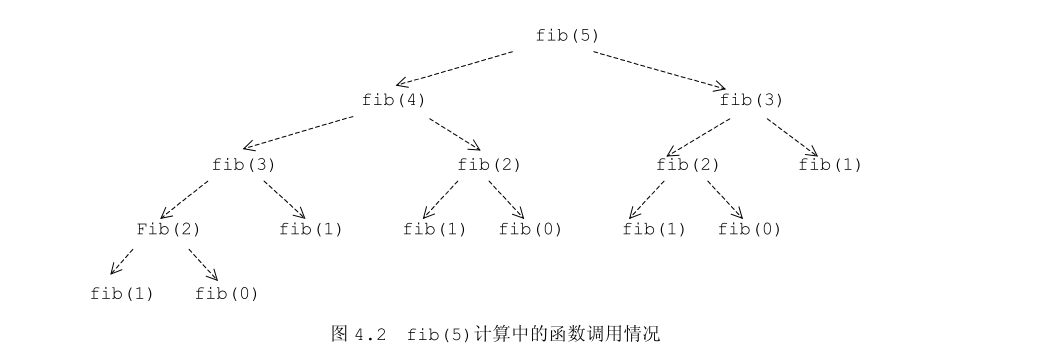
我们可以看到，很多步骤被多次重复计算，比如fib(2)就被计算了3次

更严重的问题是，参数值增加 1，函数 fib 的计算时间将为原来的 1.6 倍左右（这是理
论估计，实际时间可能更多）。

我们来对比一下这两段代码，第一段代码确实比第二段代码好吗？

不知道你知不知道大O表示法，这是由某不知名高老头提出的记法，用来估算算法的时间复杂度的一种符号。

当问题规模为n时，用这种表示方法，前者的时间复杂度为O(n)，后者的时间复杂度近似为O(2^n)

之所以说是近似，后者的时间复杂度其实和fib(n)相关，感兴趣的话可以查阅这篇论文和讨论以及这篇知乎文章

这样看来，从时间上来看，第一种方案显然更好，但是从代码的美感上来说，前者需要维护的状态过多，不如递归解法直观

什么是代码的美呢？

这其实是一个很主观的感受，以树的后序遍历为例，下面是递归和非递归的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class TreeNode(var _value: Int = 0) {
  var value: Int = _value
  var left: TreeNode = _
  var right: TreeNode = _
}

def postorderTraversal(root: TreeNode): List[Int] = {
  if (root == null) Nil
  else postorderTraversal(root.left) ++ postorderTraversal(root.right) :+ root.value
}

def postorderTraversal2(root: TreeNode): List[Int] = {
  import scala.collection.mutable
  val s = mutable.Stack[TreeNode]()
  val res = mutable.ListBuffer[Int]()
  if (root == null) return res.toList
  s.push(root, root)
  while (s.nonEmpty) {
    val node = s.pop()
    if (s.nonEmpty && node == s.top) {
      if (node.right != null)
        s.push(node.right, node.right)
      if (node.left != null)
          s.push(node.left, node.left)
    } else {
      res += node.value
    }
  }
  res.toList
}

我个人觉得前者可读性更强。

优美和性能，我全都要

有没有办法可以兼顾递归的简洁和循环迭代的效率呢？

其实用尾递归可以让编译器帮我们自动把它转换成循环的形式，同时还不影响性能(附带地还避免了栈溢出的错误)

scala编译这么慢怎么想都是你们的错，自己偷懒让编译器干活

只要简单的做个『包装』就行了

1
2
3
4
5
6
7
8
def fib(n: Int): Int = {
  @scala.annotation.tailrec
  def f(n: Int, a: Int = 0, b: Int = 1): Int = {
    if (n == 0) a 
    else f(n-1, b, a+b)
  }
  f(n)
}

关于尾递归的的实现，很难找到相关资料，下面是我用Intellij IDEA 2020.1.4 的反编译上面的代码到Java，只摘取关键部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int fib(final int n) {
    return this.f$1(n, f$default$2$1(), f$default$3$1());
}

private final int f$1(final int n, final int a, final int b) {
    while(n != 0) {
       int var10000 = n - 1;
       int var10001 = b;
       b += a;
       a = var10001;
       n = var10000;
    }

    return a;
}

private static final int f$default$2$1() {
    return 0;
}

private static final int f$default$3$1() {
    return 1;
}

通过阅读反编译后的代码，我们发现，编译器帮我们把递归形式的代码，等价展开成迭代形式的代码

所谓外递归内迭代，这样就两全其美了

什么是奇技淫巧啊

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def fib(n: Int): Int = {
  case class Memo[A, B](f: A => B) extends (A => B) {
    import scala.collection.mutable
    private val cache = mutable.Map[A, B]()
    def apply(a: A): B = cache.getOrElseUpdate(a, f(a))
  }

  lazy val f: Memo[Int, Int] = Memo {
    case n: Int if n < 2 => n
    case n: Int => f(n-1) + f(n-2)
  }

  f(n)
}

这段代码实现了不使用尾递归的方式，也能把递归的代码优化到O(n)时间复杂度

思路是计算过程中，额外开辟一个空间存放中间结果

后续计算时，如果需要的结果已经计算完成，就能直接取来用

一点范围的扩展

目前为止，我们的代码对于较小的测试样例表现良好，但是对于更大的输入呢？

fib(100)的准确值是多少？

如果你把上面的代码照搬，直接输入的话

1
2
scala> fib(100)
val res4: Int = -980107325

显然，计算的结果溢出了Int能表示的范围

这里还是稍微花点时间，讲解下显然背后的原理

所谓补码

计算机的底层存储，是按位(bit)来存的，每一个位有两个状态，0和1，在电路上分别对应低电平和高电平

假如我们用2bit来表示一个整数

首位 末位 代表的数
0 0 0
0 1 1
1 0 2
1 1 3

这就是无符号整数，只能表示非负数

如果想要表示负数，我们可以简单的偏移一个量(-2)，这样可以让正负数的量尽可能均匀

首位 末位 代表的数
0 0 -2
0 1 -1
1 0 0
1 1 1

这样表示上是没有问题了，但是计算上不方便

举个例子，这套系统应该能表示-2 ~ 1范围内的运算，那么

-1(01) + -1(01) = -2(00)

括号内为我们使用的编码，括号外为需要计算的数字

01 + 01 = 10 才对，编码对不上

不过，这难不倒聪明的前人，只要稍加修改下编码方案，就能让符号位也能正常参与运算

首位 末位 代表的数
0 0 0
0 1 1
1 0 -2
1 1 -1

-1(11) + -1(11) = -2(10)

这就是所谓的补码

我们使用的Int数据类型，也是用补码来实现的，使用了32bit来存储，所以能表示的范围是 -2^31 ~ 2^31 -1

所谓溢出，就是指运算超过能表示的范围，观察下下面的例子你就明白了

1
2
3
4
5
6
7
8
9
10
11
scala> val a = 1<<16
val a: Int = 65536

scala> a * a
val res70: Int = 0

scala> val b = 1<<31
val b: Int = -2147483648

scala> b - 1
val res71: Int = 2147483647

好了，显然内的内容讲完了

事实上，fib(47)就溢出了

1
2
3
4
5
scala> fib(46)
val res9: Int = 1836311903

scala> fib(47)
val res10: Int = -1323752223

知道问题就好办了，我们只需要增加数据能表示的范围就行了

Scala 内置的BigInt很方便就能做到这一点

1
2
3
4
5
6
7
8
9
10
11
12
def fib(n: Int): BigInt = {
  var (a, b) = (BigInt(0), BigInt(1))
  for (i <- 1 to n) {
    val temp = b
    b = a + b
    a = temp
  }
  b
}

//scala> fib(100)
//val res11: BigInt = 573147844013817084101

一个思考题：Long能存下fib(100)的结果而不溢出吗？

花枪其二

或者我们可以稍微耍个花枪，用LazyList来构造一个生成器

1
2
3
4
5
6
7
8
9
10
11
val fibs: LazyList[BigInt] = 
  BigInt(0) #:: BigInt(1) #:: (fibs zip fibs.tail).map{ t => t._1 + t._2 }

scala> fibs
val res0: LazyList[BigInt] = LazyList(<not computed>)

scala> fibs(4)
val res1: BigInt = 3

scala> fibs
val res2: LazyList[BigInt] = LazyList(0, 1, 1, 2, 3, <not computed>)

这样定义的fibs有个好处，就是懒，不问不算，但是一旦算好，结果就保存起来了

寻找失去的精度

为什么不用Double呢？根据IEEE754,双精度浮点数的精度有限

在IEEE 754标准中，用64位来存储双精度浮点数

其中分配了52位来存储浮点数的有效数字，11位存储指数，1位存储正负号

一旦需要确保精度，就会出现问题

1
2
scala> val a = 1.99999999999999999999999
val a: Double = 2.0

我们可以试下Double版本的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def fib(n: Int): Double = {
  var (a, b) = (0.0, 1.0)
  for (i <- 1 to n) {
   	val temp = b
    b = a + b
    a = temp
  }
  b
}


//scala> fib(100)
//val res73: Double = 5.731478440138172E20

// 对比BigInt版本的结果
//scala> fib(100)
//val res11: BigInt = 573147844013817084101

为了加深理解，我们来手推一遍Double的编码过程

1
2
3
4
5
6
7
def convertRadix(str: String, radix: Int, buf: String): String = {
  val i = BigInt(str)
  if (i == 0) buf.reverse
  else if (i % 2 != 0) {
  	 convertRadix((i/2).toString, radix, buf + "1")
  } else convertRadix((i/2).toString, radix, buf + "0")
}
1
2
3
令 a = 573147844013817084101
a的二进制表示 a2 = 
1 1111 0001 0010 0000 0110 0010 1111 0111 0110 1001 0000 1001 0000 0011 1000 1100 0101

图源：wikipedia

对应的公式为
$$
(-1)^{sign}(1 + \sum_{i=1}^{52}b_{52-i}2^{-i})*2^{e-1023}
$$

符号位 S： 0， 表示非负数

二进制表示：

1 1111 0001 0010 0000 0110 0010 1111 0111 0110 1001 0000 1001 0000 0011 1000 1100 0101

小数点移动后

1. 1111 0001 0010 0000 0110 0010 1111 0111 0110 1001 0000 1001 0000 0011 1000 1100 0101

移动位数E1（左移为正，右移为负）: 68

存储的阶码E，11位： 68+1023 = 1091 = (10001000011)b

尾数M，52位 （超过的截断，不足的补零）：

1111 0001 0010 0000 0110 0010 1111 0111 0110 1001 0000 1001 0000

实际存储的数据

1
2
S E            M
0 10001000011  1111 0001 0010 0000 0110 0010 1111 0111 0110 1001 0000 1001 0000

我们逆向还原下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def recover(s: Int, e: String, m: String): BigDecimal = {
  val e1 = Integer.parseInt(e, 2) - 1023
  val sign = math.pow(-1, s)
  require(m.length == 52)
  val num = 1 + (1 to 52).map(i=>(m(i-1)-'0')*BigDecimal(2).pow(-i)).sum
  println(e1, sign, num)
  BigDecimal(2).pow(e1) * sign * num
}

/*
scala>  recover(0, "10001000011", "1111000100100000011000101111011101101001000010010000")
(68,1.0,1.941900430109885888896315009333193)
val res53: BigDecimal = 573147844013817069567.9999999999999

scala> recover(0, "10001000011", "1111000100100000011000101111011101101001000010010000").toDouble
(68,1.0,1.941900430109885888896315009333193)
val res54: Double = 5.731478440138171E20

// 对比之前的结果 完全吻合

scala> fib(100)
val res73: Double = 5.731478440138172E20

*/

所以，用Double前，首先需要问自己一个问题，这个数据需不需要确保完整的精度。

所以，要二分吗

之前的问题都是求值，现在换一个问题

斐波那契数列中，第一个有 1000 位数字的是第几项（从零开始算的话）？

考虑略微修改后，复用之前的代码

1
2
3
4
5
6
7
8
9
def fib(n: Int): BigInt = {
  var (a, b) = (BigInt(0), BigInt(1))
  for (i <- 1 to n) {
    val temp = b
    b = a + b
    a = temp
  }
  a
}

一个朴素的做法是逐个试探

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
scala> fib(200).toString.length
val res80: Int = 42

scala> fib(700).toString.length
val res81: Int = 146

scala> fib(3000).toString.length
val res82: Int = 627

scala> fib(5000).toString.length
val res83: Int = 1045

scala> fib(4000).toString.length
val res84: Int = 836

...

之所以能这样做，是因为fib(n)的长度是一个随着n单调非递减的函数，我们只要对比结果

  • 比1000大，调小n再试一次
  • 比1000小，调大n再试一次
  • 正好是1000，此时n就是答案

我们使用二分法，需要确定上界和下界

显然fib(n)的长度小于n，这确定了下界

上界可以用放缩法来确定

我们知道

$$
\because fib(n) = fib(n-1) + fib(n-2) > 2×fib(n-2) \
\therefore fib(n) > 16 × fib(n-8) > 10 × fib(n-8)
$$

所以n增加8时，对应的十进制长度至少增加1

$$
len(fib(8n)) > n
$$

上界可以选择为8*n

我们可以用二分法来替代手动试探结果的过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def fibLen(x: Int): Int = {
  var left = x
  var right = 8 * x
  def len(guess: Int) = fib(guess).toString.length
  while (left < right) { 
    var guess = left + (right-left)/2
    var l = len(guess)
    if (l < x) {
      left = guess + 1
    } else if (l >= x) {
      right = guess
    }
    println(guess, l, left, right)
  } 
  left
}

/*
scala> fibLen(1000)
(6500,1359,1000,6500)
(3750,784,3751,6500)
(5125,1071,3751,5125)
(4438,928,4439,5125)
(4782,1000,4439,4782)
(4610,964,4611,4782)
(4696,982,4697,4782)
(4739,991,4740,4782)
(4761,995,4762,4782)
(4772,997,4773,4782)
(4777,998,4778,4782)
(4780,999,4781,4782)
(4781,999,4782,4782)
val res108: Int = 4782
*/

花枪其三

我们也可以暴力遍历，这个时间复杂度是可以接受的

1
2
3
4
val fibs: LazyList[BigInt] = 
  BigInt(0) #:: BigInt(1) #:: (fibs zip fibs.tail).map{ t => t._1 + t._2 }

fibs.zipWithIndex.dropWhile(_._1.toString.length<1000).head._2  // 4782

输入范围扩充

如果我们要求一个大一些的数据，比如fib(10^9)

这个数太大了，所以我们求的是 fib(10^9) % (10^9 + 7)来检验结果是否正确

即求

$$
fib(10^9) \ % \ 1000000007
$$

首先分析下问题的规模，10^9的情况下，O(n)的做法过慢，最好能有更好的算法

如果你是布鲁特佛斯的爱好者，那当我没说

普通青年：矩阵快速幂

首先需要介绍两个前置知识

  • 矩阵
  • 快速幂

矩阵

由 m × n 个数a[i][j]排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作

这里会用到一点简单的矩阵乘法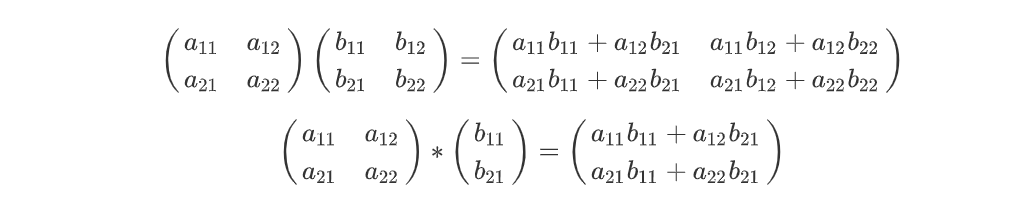

快速幂

考虑这么一个问题，求解

$$
A^n \ mod \ m
$$

模运算的乘法规则和基本四则运算类似

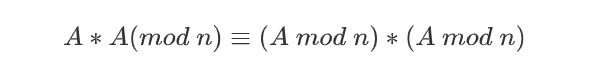
比较朴素的做法需要O(n)的时间

1
2
3
4
5
6
7
def pow(a: Long, n: Long, m: Long): Long = {
  var res = 1L
  for (i <- 1 to n) {
    res = (res * a) % m
  }
  res
}

其实我们可以利用上一步的结果来加速运算

比如，对于求A^10

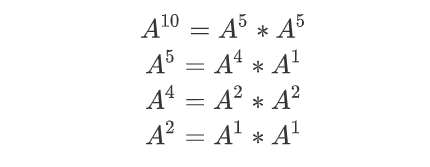
也可以写作

1
2
3
4
pow(a, 10) = pow(a^2, 5)
= a^2 * pow(a^4, 2)
= a^2 * pow(a^8, 1)
= a^2 * a^8

每次对需要计算的幂除以二向下取整，通过这样的方法，每次需要计算的幂次都是原来的一半
这样可以把时间复杂度从O(n)降低到O(logn)

1
2
3
4
5
6
7
8
9
10
11
12
13
def pow(a: Long, n: Long, m: Long): Long = {
  var res = 1L
  var i = n
  var base = a
  while (i > 0) {
    if (i % 2 != 0) {
      res = (res * base) % m
    }
    base = (base * base) % m
    i = i / 2
  }
  res
}

矩阵快速幂

有了矩阵和快速幂的前置科技，矩阵快速幂的科技被点亮就是水到渠成的了

用F(n)表示斐波那契数列的第n项

考虑构造一个矩阵

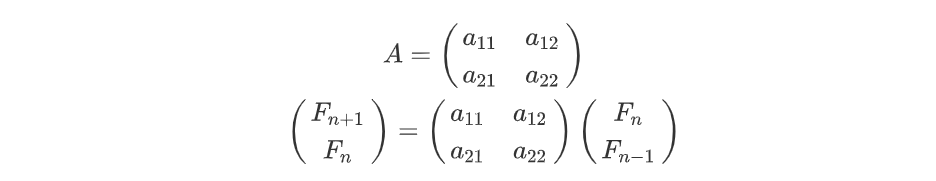
如果能找(gou)到(zao)这样的矩阵A，把左右两边看成递推数列，有

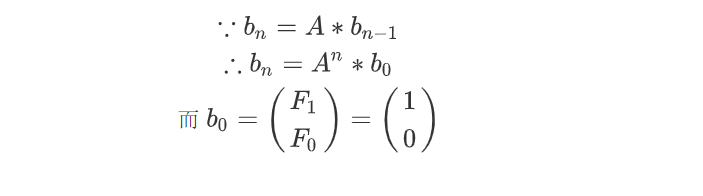
依据矩阵的乘法，可知

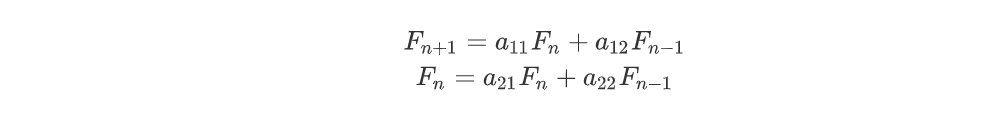
由斐波那契数列的递归式，可知
$$
F_{n+1} = F_n + F_{n-1} ，\
F_{n} = F_n
$$

比较系数后，可以求出矩阵A

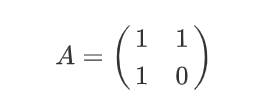
于是，可以得出

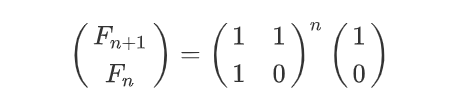
因此，只要求出A^n 就能知道第N项的斐波那契数列

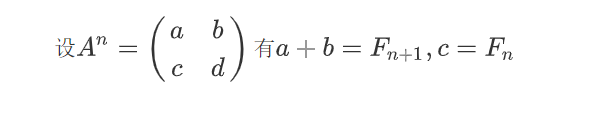
这个求幂运算可以利用之前快速幂的算法，依葫芦画瓢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
final case class Matrix(elements: Array[Array[Long]], M: Long = 1000000007) {
  val rows: Int = elements.length
  val cols: Int = elements.headOption.getOrElse(Array.empty[Long]).length

  def *(that: Matrix): Matrix = {
    require(this.cols == that.rows, "invalid matrix size")
    val res = Array.fill(this.rows, that.cols)(0L)
    for (i <- 0 until this.rows; j <- 0 until that.cols)
      for (k <- 0 until this.cols) {
        res(i)(j) = (res(i)(j) + this.elements(i)(k) * that.elements(k)(j)) % M
      }
    Matrix(res)
  }

  def ^(power: Int): Matrix = {
    require(power >= 0, "power should not be negative")

    val unitElements = Array.fill(this.rows, this.cols)(0L)
    for ((i, j) <- (0 until this.rows) zip (0 until this.cols)) unitElements(i)(j) = 1L
    val unitMatrix = Matrix(unitElements)

    @scala.annotation.tailrec
    def fastPow(res: Matrix, p: Int, base: Matrix): Matrix = {
      if (p == 0) res
      else if (p % 2 == 0) fastPow(res, p/2, base * base)
      else fastPow(res * base, p/2, base * base)
    }

    fastPow(unitMatrix, power, this)
  }
}

简单测试下,速度还是很快的

1
2
3
4
5
6
7
8
scala> val A = Matrix(Array(Array(1L,1L), Array(1L,0L)))
val A: Matrix = Matrix([[J@5e85c21b,1000000007)

scala> def fib(n: Int) =  (A^n).elements(1)(0)
def fib(n: Int): Long

scala> fib(1000000000)
val res7: Long = 21

文艺青年：快速倍增法

矩阵快速幂的算法的时间复杂度是O(m^3*logn)级别的，这里的m计算两个m长度的数乘积所需要的时间

其实，有一个速度更快的方案，我们可以略过矩阵计算这一步骤

一个朴素的思路是，观察并猜出斐波那契数列的2*2矩阵表达形式，然后用数学归纳法证明

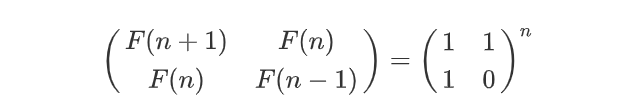
对上述式子做一个变换

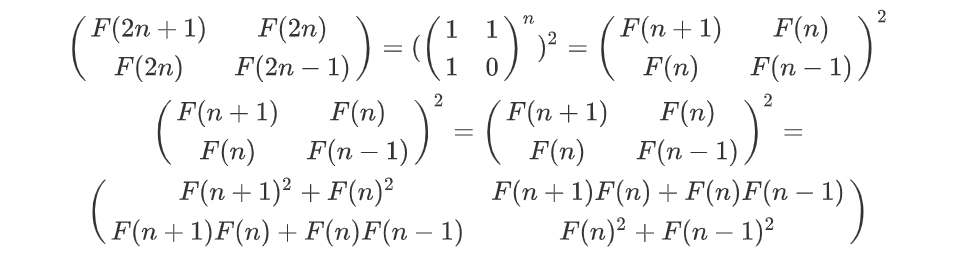
由左右两个矩阵间的对应关系，可得

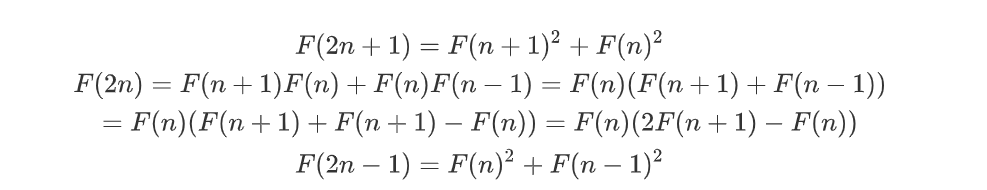
我们需要用到也就是

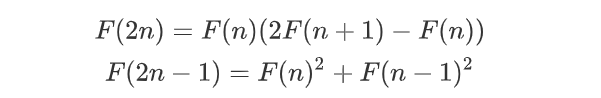
有了这两个式子，我们能从F(n), F(n-1) 计算出 F(2n)，F(2n-1)

1
2
3
4
5
6
7
8
9
10
def fastFib(n: Int, M: Long = 1000000007): (Long, Long) = {
  if (n == 0) (0L, 1L)
  else {
    val p = fastFib(n / 2)
    val a = p._1 * ((2 * p._2  - p._1) % M + M) % M
    val b = (p._1 * p._1 + p._2 * p._2) % M
    if (n % 2 == 0) (a, b)
    else (b, (a + b) % M)
  }
}

这里之所以要(... % M + M)，是为了防止中间过程出现负数

简单试验下

1
2
scala> fastFib(1000000000)._1
val res64: Long = 21

二逼青年： 扩充数域

一个化归的笑话

如果不懂什么矩阵，也不懂什么数学归纳法，更不懂什么生成函数，能不能用初等方法求出答案呢？

首先我们需要前置知识：斐波那契数列的通项公式推导

在此之前，我们先来解决递推式的一般推导问题

$$
x_n = ax_{n-1}, x_0 = C, a ≠ 0
$$

这个式子很好求通项公式，观察到下一项是上一项的倍数，所以有

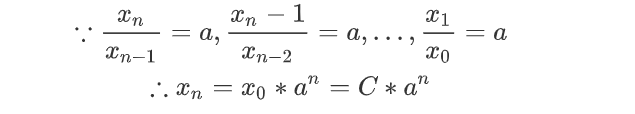
一天，数学家觉得自己已受够了数学，于是他跑到消防队去宣布他想当消防员。
消防队长说：「您看上去不错，可是我得先给您一个测试。」
消防队长带数学家到消防队后院小巷，巷子里有一个货栈，一只消防栓和一卷软管。
消防队长问：「假设货栈起火，您怎么办？」
数学家回答：「我把消防栓接到软管上， 打开水龙头，把火浇灭。」
消防队长说：「完全正确。最后一个问题：假设您走进小巷，而货栈没有起火，您怎么办？」
数学家疑惑地思索了半天，终于答道：「我就把货栈点着。」
消防队长大叫起来：「什么？太可怕了，您为什么要把货栈点着？」
数学家回答：「这样我就把问题化简为一个我已经解决过的问题了。」

好了，有了这一问的基础，我们加大点难度，尝试更加一般的结论

$$
y_n=ay_{n-1} + b, y_0 = C
$$

如果这个式子的左右两边能化归到第一问等比的形式，就好求了

$$
(y_n + t) = a(y_{n-1} + t)
$$

展开后可以求出

$$
\because y_n = ay_{n-1} + (a-1)t \
\therefore b = (a - 1)t, t = \frac{b}{a-1} \
$$

这里要注意一个问题，分母不能为0，所以对a=1的情况要额外讨论，当a=1时，原式便退化成了等差数列

$$
\because y_n = y_{n-1} + b
\therefore y_n = C + nb
$$

当a不为1时

$$
\frac{y_n + \frac{b}{a-1}}{y_{n-1} + \frac{b}{a-1}} = a \
由第一问的结论可知 \
y_n + \frac{b}{a-1} = (C + \frac{b}{a-1}) * a^n
$$

综上所述

$$
y_n=\begin {cases}
(C + \frac{b}{a-1}) * a^n - \frac{b}{a-1}, & a ≠ 1 \\
C + nb, & a = 1
\end {cases}
$$

说了这么多，让我们回到原来的问题

$$
F_n = F_{n-1} + F_{n-2}, F_0 = 0, F_1 = 1
$$

我们希望求出上面这个问题的一般解

有了两问的铺垫，我们知道可以用构(cou)造的方法化归到已知的问题

对于

$$
y_n=ay_{n-1} + b, y_0 = C
$$

我们知道其通项公式为

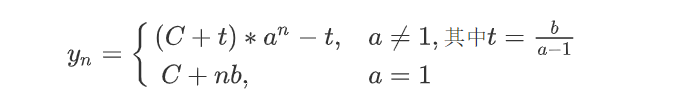
我们的目标希望整理出如下的式子

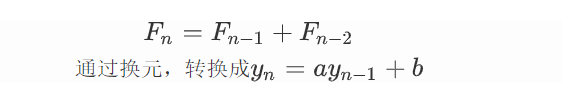
使用待定系数法

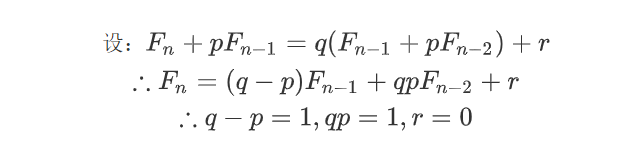
由一元二次方程，可知
$$
\begin {cases}
p = \frac{-1-\sqrt5}{2} \\
q = \frac{1-\sqrt5}{2}
\end {cases} 或者
\begin {cases}
p = \frac{\sqrt5-1}{2} \\
q = \frac{\sqrt5+1}{2}
\end {cases}
$$

接着

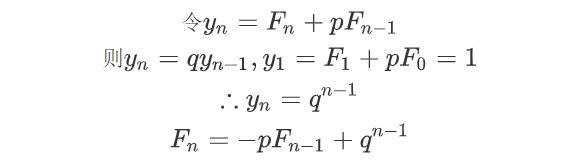
右边不是常数，无法直接使用第二问的结论，没关系，我们继续凑

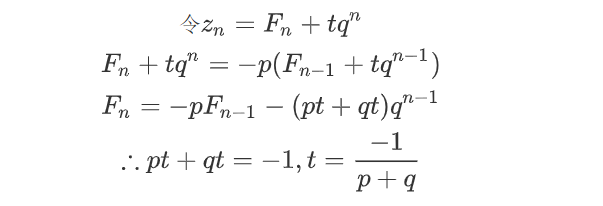
所以

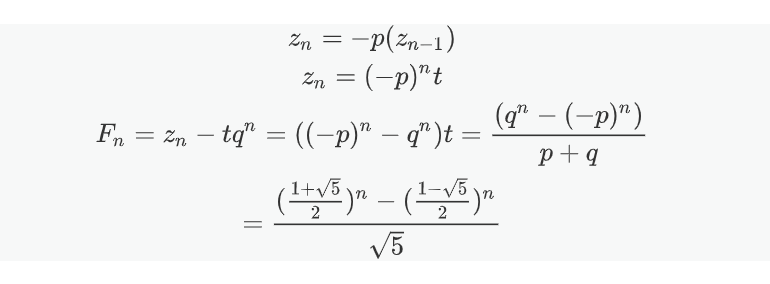
为了便于书写，我们做如下约定
$$
a = \frac{1+\sqrt5}{2}, b=\frac{1-\sqrt5}{2}
$$

那么

$$
F_n = \frac{1}{\sqrt 5}(a^n - b^n)
$$

一点简单的数论

对于求模运算，由于a, b的分母都为2，首先需要找到2在1000000007的模逆元

方法有很多，这里直接给出结果500000004

我们知道，斐波那契的每一项都是整数，因而尽管上面的式子中有无理数，但是这一部分都是会被互相抵消的

为了不丢失精度，将无理数看作类似复数的东西，设

$$
m + n \sqrt 5 记作 数对<m, n>，其中m,n都为整数 \
M = 1000000007 \
t = 500000004
$$

那么

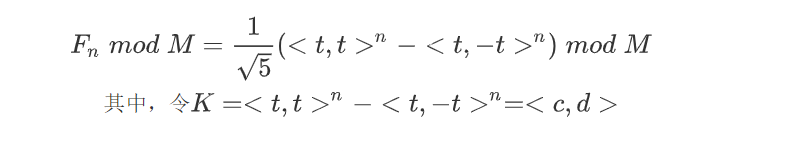
承前所言，无理数部分会抵消，所以c一定为0,我们关心的就是d的值

接下来我们需要定义数对在模意义下的运算

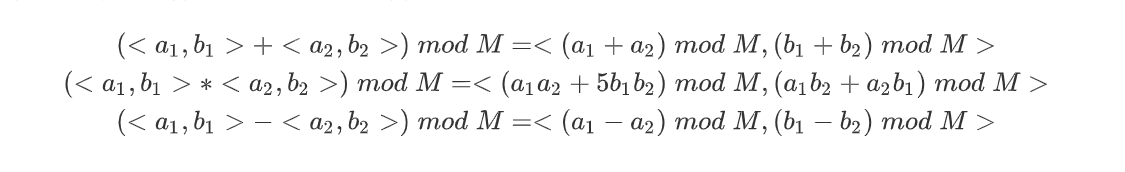
幂运算的部分一样可以套用快速幂的思路，不同的是，这里不存在单位元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
final case class ExPair(a: Long, b: Long, M: Long = 1000000007) {
  def +(that: ExPair): ExPair = {
    ExPair((this.a + that.a) % M, (this.b + that.b) % M)
  }

  def *(that: ExPair): ExPair = {
    val na = (this.a * that.a + 5 * this.b * that.b) % M
    val nb = (this.a * that.b + this.b * that.a) % M
    ExPair(na, nb)
  }

  def -(that: ExPair): ExPair = {
    ExPair((this.a - that.a + M) % M, (this.b - that.b + M) % M)
  }

  def ^(power: Int): ExPair = {
    require(power >= 1, "power should be positive")

    @scala.annotation.tailrec
    def fastPow(res: Option[ExPair], p: Int, base: ExPair): ExPair = {
      if (p == 0) res.get
      else if (p % 2 == 0) {
        fastPow(res, p/2, base * base)
      }
      else {
        if (res.isDefined) fastPow(Some(res.get * base), p/2, base * base)
        else fastPow(Some(base), p/2, base * base)
      }
    }

    fastPow(None, power, this)
  }
}

和之前的结果做一个交叉检验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
scala> val T = 500000004
val T: Int = 500000004

scala> val A = ExPair(T, T)
val A: ExPair = ExPair(500000004,500000004,1000000007)

scala> val B = ExPair(T, -T)
val B: ExPair = ExPair(500000004,-500000004,1000000007)

scala> def fib(n: Int) = ((A^n)-(B^n)).b
def fib(n: Int): Long

scala> (1 to 10).map(fib)
val res47: IndexedSeq[Long] = Vector(1, 1, 2, 3, 5, 8, 13, 21, 34, 55)

scala>  fib(1000000000)
val res48: Long = 21

Googol的斐波那契

某著名搜索引擎的来源，就是单词Googol，起名字还真是要有品味的，不然就像这样

​*图片来源*

或者拿古希腊神仙名字来命名

现在新的问题来了，求斐波那契数列的第Googol项，即

$$
F(10^{100}) mod (10^9 + 7)
$$

这里需要一点简单的幂运算知识

$$
A^{p+q} = A^pA^q \
A^{p·q} = (A^p)^q \
A^{p^q} = A^{p^{q-1}·p}
= (A^{p^{q-1}})^p = \dots \
= \underbrace{(((A^p)^p)\dots)^p)^p}_{q个}
$$

依据这个思路，写起来就不难了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 复用之前方法
final case class Matrix(elements: Array[Array[Long]], M: Long = 1000000007) {
  val rows: Int = elements.length
  val cols: Int = elements.headOption.getOrElse(Array.empty[Long]).length

  def *(that: Matrix): Matrix = {
    require(this.cols == that.rows, "invalid matrix size")
    val res = Array.fill(this.rows, that.cols)(0L)
    for (i <- 0 until this.rows; j <- 0 until that.cols)
      for (k <- 0 until this.cols) {
        res(i)(j) = (res(i)(j) + this.elements(i)(k) * that.elements(k)(j)) % M
      }
    Matrix(res)
  }

  def ^(power: Int): Matrix = {
    require(power >= 0, "power should not be negative")

    val unitElements = Array.fill(this.rows, this.cols)(0L)
    for ((i, j) <- (0 until this.rows) zip (0 until this.cols)) unitElements(i)(j) = 1L
    val unitMatrix = Matrix(unitElements)

    @scala.annotation.tailrec
    def fastPow(res: Matrix, p: Int, base: Matrix): Matrix = {
      if (p == 0) res
      else if (p % 2 == 0) fastPow(res, p/2, base * base)
      else fastPow(res * base, p/2, base * base)
    }

    fastPow(unitMatrix, power, this)
  }
  
  // 新加的
  def ^^(p: Int, q: Int): Matrix = {
    require(p>0 && q>0, "power parameters, p and q, should be positive")
    (1 until q).foldLeft(this ^ p)((cur: Matrix, _) => cur ^ p)
  }
}


// fib(p^q)
def fibPQ(p: Int, q: Int) = fastFib(p)._1

验证下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
scala> val A = Matrix(Array(Array(1L,1L), Array(1L,0L)))
val A: Matrix = Matrix([[J@73ba068e,1000000007)

scala> def fibPQ(p: Int, q: Int) =  (A^^(p,q)).elements(1)(0)
def fibPQ(p: Int, q: Int): Long

scala> fibPQ(10, 9)
val res49: Long = 21

scala> fibPQ(10, 100)
val res50: Long = 175077019

scala> fibPQ(10, 1000)
val res51: Long = 552179166

扩展阅读

  • 现有的浮点运算是基于二进制的，有没有十进制的呢
  • 基于斐波那契的数据结构，Fib堆
  • 基于斐波那契的算法，Fib搜索
  • 求解逆元时常用的算法，扩展欧几里得(ex-gcd)以及费马小定理
  • 求解常系数线性齐次递推关系，参考《离散数学》8.2.2小节
  • Karatsuba乘法

P.S 图有点糊，因为部分公式是直接贴的图而不是渲染的

我现在暂时还没想到好办法来处理 mathjax和hexo冲突导致的渲染问题

本文对应的pdf版可以在这里获取

参考链接

  1. WikiPedia: Fibonacci number
  2. OI-wiki: fibonacci
  3. Github: 我们为什么要考斐波那契数列？一道上机笔试题的解析，兼谈技术面试和编程基本功
  4. 博客园: 【学习笔记】斐波那契数列的简单性质
  5. Fast Fibonacci algorithms
  6. CSDN: float和double的编码示例
  7. 知乎：斐波那契数列通项公式是怎样推导出来的？ - Lancewu的回答
  8. 人民教育出版社-课程教材研究所：斐波那契数列的通项公式推导