FPDIS 1.For Expressions and Monads

前言

这一系列的课程是Scala专项课程的第二部分，课程名为Functional Program Design in Scala

这里我就把它简写成FPDIS了,和之前记录的笔记一样，这个系列也会记录对应的心得体会以备后续自查

Recap: Functions and Pattern Matching

{
  "firstName": "John",
  "lastName": "Smith",
  "isAlive": true,
  "age": 27,
  "address": {
    "streetAddress": "21 2nd Street",
    "city": "New York",
    "state": "NY",
    "postalCode": "10021-3100"
  },
  "phoneNumbers": [
    {
      "type": "home",
      "number": "212 555-1234"
    },
    {
      "type": "office",
      "number": "646 555-4567"
    }
  ],
  "children": [],
  "spouse": null
}

上面这个JSON（JavaScript Object Notation ）在Scala中可以这样表示

abstract class JSON
case class JSeq(elems: List[JSON]) extends JSON
case class JObj(bindings: Map[String, JSON]) extends JSON
case class JNum(num: Double) extends JSON
case class JStr(str: String) extends JSON
case class JBool(b: Boolean) extends JSON
case object JNull extends JSON

假如说我现在有了一段JSON的数据在内存里，如何按照格式把他展开成字符串呢?

def show(json: JSON): String = json match {
  case JSeq(elems) =>
    elems.map(show).mkString("[", ",", "]")
  case JObject =>
    val assocs = bindings.map{
      case (key, value) => s""""${key}":{show(value)}"""
    }
    assocs.mkString("{", ",","}")
  case JNum => num.toString
  case JStr =>  "\"" + str + "\""
  case JBool => b.toString
  case JNull => "null"
}

下面一段desugar的代码有助于理解Scala编译器的工作

比如说，当我们看到上面这段构造匿名函数的代码时，其实是什么样子的类型呢？

{case (key, value) => key + ":" + show(value)}

其实这段的类型是(String, JSON) => String

desugar后就是new Function1[(String, JSON) => String]

其中type JBinding = (String, JSON)

其中Function1的签名为

trait Function1[-A, +R] {
  def apply(x: A): R
}

这里泛型A/R签名的-/+符号是用来指示对应的型变，这个Martin说会在后续的课程中详细说明（划重点）

这么一来，我们可以把上面的那段代码进行展开

// {case (key, value) => key + ":" + show(value)}
new Function1[JBinding, String] {
  def apply(x: JBinding): String = x match {
    case (key, value) => key + ":" + show(value)
  }
}

类似地有

trait Map[Key, Value] extends (Key => Value)
trait Seq[Elem] extend (Int => Elem)

上面地例子由于没有实现对应的JSON类，下面用一个具体的例子来演示

val f: String => String = {case "ping" => "pong"}

scala> f("ping")
val res2: String = pong

scala> f("abc")
scala.MatchError: abc (of class java.lang.String)
  at $anonfun$f$1(<console>:1)
  ... 32 elided

对于不存在与定义域内的输入，会抛出异常，但是可以通过PartialFunction来预先确认是否有定义

val f: String => String = {case "ping" => "pong"}

scala> val f: PartialFunction[String, String] = {case "ping" => "pong"}
val f: PartialFunction[String,String] = <function1>

scala> f.isDefinedAt("abc")
val res6: Boolean = false

scala> f.isDefinedAt("ping")
val res7: Boolean = true

PartialFunction对应的函数签名如下

trait PartialFunction[-A, +R] extends Function[-A, +R] {
  def apply(x: A): R
  def isDefinedAt(x: A): Boolean
}

所以，对于上述的代码，会被展开成

new PartialFunction[String, String] {
  def apply(x: String): String = {
    case "ping" => "pong"
  }
  
  def isDefinedAt(x: String): Boolean = {
    case "ping" => true
    case _ => false
  }
}

本小节最后附有练习若干

val f: PartialFunction[List[Int], String] = {
  case Nil => "one"
  case x :: y :: rest => "two"
}

对于以上函数，f.isDefinedAt(List(1,2,3))的输出是什么

• true
• false

对于下面的函数

val g: PartialFunction[List[Int], String] = {
  case Nil => "one"
  case x :: rest => 
    rest match {
      case Nil => "two"
    }
}

g.isDefinedAt(List(1,2,3))的输出是什么

• true
• false

这两个练习可以看出，

PartialFunction只能保证在最外层的match case 中是否存在定义，

不能保证一定有对应的结果

Recap: Collections

对于简单的for-yield语句，直接会翻译成map

// for (x <- e1) yield e2
e1.map(x => e2)

如果在for语句中有if条件，那么会加上filter

// for (x <- e1 if f; s) yield e2
for (x <- e1.withFilter(f); s) yield e2

这里是withFilter，它是lazy的，所以不会立刻计算

对于多重循环的情况

// for (x <- e1; y <- e2; s) yield e3
e1.flatMap(x => for(y <- e2; s) yield e3)

可以把for循环和模式匹配(pattern matching)一起使用

val data: List[JSON] = ...
for {
  JObj(bindings) <- data
  JSeq(phones) <- bindings("phoneNumbers")
  JObj(phone) <- phones
  JStr(digits) <- phone("number")
  if digits startsWith "212"
} yield (bindings("firstName"), bindings("lastName"))

上面这段语句提取出json中，会提取出所有的以”212”开头的电话号码的记录的姓和名

对于其中的模式匹配，编译器会这样翻译

// pat <- expr

x <- expr withFilter {
  case pat => true
  case _ => false
} map {
  case pat => x
}

本小节的练习

for {
  x <- 2 to N
  y <- 2 to x
  if (x % y == 0)
} yield (x, y)

这段代码会翻译成什么呢

(2 to N).flatMap(x => for(y <- 2 to x if x % y == 0) yield (x, y))
= (2 to N).flatMap(x => (2 to x).withFilter(y => x % y == 0).map(y => (x, y)))

Querys with For

这一小节简单讲解了下如何用For来对数据结构进行查询和调优

Translation of For

这一小节基本上是第二小节的重复

Functional Random Gererators

构造随机整数很简单

import java.util.Random
val rand = new Random
rand.nextInt

如果我们想要用更加通用的方法来生成随机数，该怎么做呢

trait Generator[+T] {
  def generate: T
}

val integers = new Generator[Int] {
  val rand = new java.util.Random
  def generate: Int = rand.nextInt
}

val booleans = new Generator[Boolean] {
  def generate: Boolean = integers.generate > 0
}

val pairs = new Generator[(Int, Int)] {
  def generate: Boolean = (integers.generate, integers.generate)
}

这样写的确没什么问题，就是每次都需要写重复的代码，那么可以不可以避免这一点呢

trait Generator[+T] {
  self => // an alias for "this"
  def generate: T
  
  def map[S](f: T => S): Generator[S] = new Generator[S] {
    def generate = f(self.generate)
  }
  
  def flatMap[S](f: T => Generator[S]): Generator[S] = new Generator[S] {
    def generate = f(self.generate).generate
  }
}

这里之所以要在外层声明self，是因为，如果不这样做，f(generate)就会被解释成f(this.generate)。在这个函数中this在map里，this.generate就会导致循环调用，为了能够获取到外部的generate，所以事先要声明self type

有了这些准备工作，我们就能直接用for来方便地写代码了

val integers = new Generator[Int] {
  val rand = new java.util.Random
  def generate: Int = rand.nextInt
}

val booleans = for (x <- integers) yield x > 0

这里可以把booleans部分展开

val booleans = integers.map{ x => x > 0}

val booleans = new Generator[Boolean] {
  def generate = ((x: Int) => x > 0)(integers.generate)
}

val booleans = new Generator[Boolean] {
  def generate = integers.generate > 0
}

是不是和最开始的一样了？

如法炮制

def pairs[T, U](t: Generator[T], u: Generator[U]) = t flatMap {
  x => u map {y => (x, y)}
}

def pairs[T, U](t: Generator[T], u: Generator[U]) = for {
  x <- t
  y <- u
} yield (x, y)

// 完全展开
def pairs[T, U](t: Generator[T], u: Generator[U]) = new Generator[(T,U)] {
  def generate = (new Generator[(T, U)] {
    def generate = (t.generate, u.generate)
  }).generate
}

// 化简
def pairs[T, U](t: Generator[T], u: Generator[U]) = new Generator[(T,U)] {
  def generate = (t.generate, u.generate)
}

有了这些，我们可以方便的写一些辅助函数

def single[T](x: T): Generator[T] = new Generator[T] {
  def generate = x
}

def choose(lo: Int, hi: Int): Generator[Int] = 
  for (x <- integers) yield lo + (x % (hi - lo) + hi - lo) % (hi - lo)

def oneOf[T](xs: T*): Generator[T] = 
  for (idx <- choose(0, xs.length)) yield xs(idx)

这样我们可以任意生成随机的List

// 以下代码并不能REPL编译过， 需要把之前的代码一起放文件里才能运行
// 或者在REPL中以":paste"模式粘贴包括之前依赖的所有代码
def lists: Generator[List[Int]] = for {
  isEmpty <- booleans
  list <- if (isEmpty) emptyLists else nonEmptyLists
} yield list

def emptyLists = single(Nil)

def nonEmptyLists =  for {
  head <- integers
  tail <- lists
} yield head :: tail

本小节的练习是实现Tree的构造器

trait Tree

case class Inner(Left: Tree, Right: Tree) extends Tree

case classs Leaf(x: Int) extends Tree

def leafs: Generator[Leaf] = for {
  x <- integers
} yield Leaf(x)

def inners: Generator[Inner] = for {
  l <- trees
  r <- trees
} yield Inner(l, r)

def trees: Generator[Tree] = for {
  isLeaf <- booleans
  tree <- if (isLeaf) leafs else inners
} yield tree

那么这类生成器到底有什么用处呢？

一个显然的想法就是用这些生成器来构造随机的测试数据

package testtools
import generator.Generators.{pairs, lists}
import generator.Generator

object Test {
  def test[T](g: Generator[T], numTimes: Int = 100)
             (test: T => Boolean): Unit = {
    for (i <- 0 until numTimes) {
      val value = g.generate
      assert(test(value), s"$i test: test failed for $value")
    }
    println(s"passed $numTimes tests")
  }

  def main(args: Array[String]): Unit = {
    test(pairs(lists, lists)) {
      case (xs, ys) => (xs ++ ys).length >= xs.length
    }
  }
}

Monads

​ 简单的说单子就是自函子范畴上的一个幺半群

前面的省略都是为了能有更多的篇幅来啃Monad

让我们抛开数学范畴论的术语，直接从代码上来讲解

trait M[T] {
  def flatMap[U](f: T => M[U]): M[U]
}

def unit[T](x: T): M[T]

Monad是包含flatMap操作和unit单位元的数据结构

unit可以让我们把任意元素转换到Monad中

flatMap可以让我们对Monad中的元素进行运算

这样也许过于抽象，下面是一些符合Monad性质的数据结构

• List —— unit(x) = List(x)
• Set —— unit(x) = Set(x)
• Option —— unit(x) = Some(x)
• Generator —— unit(x) = single(x)

flatMap是以上所有数据结构都有的方法，它们之间的区别就是unit不同

map也可以由flatMap和Unit来表示

m map f == m flatMap (x => unit(f(x)))
        == m flatMap (f andThen unit)

下面我们来介绍更严格的Monad定义

当一个类型(数据结构)满足下面三个条件时，我们将之称为Monad

1. 结合律

   m flatMap f flatMap g == m flatMap (x => f(x) flatMap g)

2. 存在左单位元

   unit(x) flatMap f == f(x)

3. 存在右单位元

   m flatMap unit == m

下面用例子来具体说明上面的性质

// 这里由于和自带的关键字同名，所以无法编译，意会就行
abstract class Option[+T] {
  def flatMap[U](f: T => Option[U]): Option[U] = this match {
    case Some(x) => f(x)
    case None => None
  }
}

下面简单证明下符合以上三条性质

1.
∵ Some(x) flatMap f == f(x)

∴ 存在左单位元

2.
∵ opt flatMap Some == 
opt match {
  case Some(x) => Some(x)
  case None => None
}

无论opt为Some(x)还是None结果都为 opt flatMap Some == opt

∴ 存在右单位元

3.
对于式子 m flatMap f flatMap g == m flatMap (x => f(x) flatMap g)
左边 = opt flatMap f flatMap g == 
opt match {
  case Some(x) => f(x)
  case None => None
} match {
  case Some(x) => g(x)
  case None => None
} == 
opt match {
  case Some(x) => g(f(x))
  case None => None
}


右边 = opt flatMap (x => f(x) flatMap g) ==
opt match {
  case Some(x) => f(x) flatMap g
  case None => None
}

而 f(x) flatMap g == g(f(x))
∴左边=右边
结合律满足

看完上面这一通证明，你也许会好奇，这到底有什么用？
有了上面的例子，下面的转换也就更容易理解了

// 结合律的性质有利于任意变换嵌套for循环的计算顺序
for {
  y <- for (x <- m y<- f(x)) yield y
  z <- g(y)
} yield z ==
for {
  x <- m
  y <- f(x)
  z <- g(y)
}

// 右单位元
for (x <- m) yield x == m

// 左单位元在for循环中没有对应的表示

接下来再介绍一个“Monad”类型Try，函数签名如下

abstract class Try[+T] {
  def flatMap[U](f: T => Try[U]): Try[U] = this match {
    case Success(x) => try f(x) catch {case ex: Exception => Failure(ex)}
    case fail: Failure => fail
  }
  
  def map[U](f: T => U): Try[U] = this match {
    case Success(x) => Try(f(x))
    case fail: Failure => fail
  }
}

case class Success[T](x: T) extends Try[T]
case class Failure(ex: Exception) extends Try[Nothing]

object Try {
  def apply[T](expr: => T): Try[T] = {
    try Success(expr)
    catch {
      case ex: Exception => Failure(ex)
    }
  }
}

这里用了call by name的传入参数方式，这样不会立刻计算expr

对于下面的使用

for {
  x <- computeX
  y <- computeY
} yield f(x, y)

如果computeX和computeY都成功调用，那么返回的结果是Success(x)和Success(y)

如果任意一个调用失败，都会返回Failture(ex)

事实上，如果按照那三条规则检验，就会发现

Try(expr) flatMap f != f(expr)

左边不会抛出异常，而右边会

但是这个能和For很好的配合

有的时候，不需要完全符合三条性质也能使用，更深的理解就配合使用来加深印象吧

作业QuickCheck

作业的代码下载地址为：http://alaska.epfl.ch/~dockermoocs/handouts-coursera-2.13/quickcheck.zip

下面是一个纯函数式(不对数据进行修改)的堆的实现

具体的论文地址为：http://www.brics.dk/RS/96/37/BRICS-RS-96-37.pdf

二项式队列

二项式队列是由树组成的

binomial tree递归定义如下

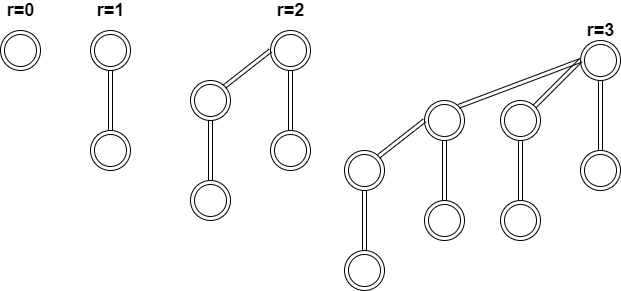
• rank 为 0 的binomial tree是单节点
• rank 为 r+1 的binomial tree是由两个 rank 为 r 的binomial tree连接组成，假如我们把这两个rank为r的binomial tree称为a,b。其中连接方式为，a的根节点连接到b的根节点的最左边的子节点的位置

一图胜万言

从这个定义里，可以显然发现，rank r的binomial tree有2^r个节点

除了上面的递归定义外，还有一个更方便的定义来描述binomial tree

rank r 的树有r个子节点 t1 t2 … tr , 其中ti 是一个rank (r-i) 的binomial tree

一个binomial tree，如果对于它的所有节点，都满足父节点小于等于其子节点，那么我们说这个binomial tree是已经堆有序(heap-ordered)的

为了在连接两个binomial tree时维护堆有序的状态，我们将根较大的树设为根较小的树的子树。

一个二项式队列是一个由堆有序的binomial tree组成的森林，这个森林中，任意两个binomial tree都有着不同的rank

举个例子，一个大小为21的二项式队列，21的二进制表示为10101，所以这个二项式队列是由rank 0, rank 2, rank4 的binomial tree组成的

我们现在已经做好了描述二项式队列各项操作的准备。因为在二项式队列中，所有的树都已经是堆有序的了

对于一个有n个节点的二项式队列，最多包含
$$
k = \lfloor log_2{(n+1)} \rfloor
$$
个树

我们知道，二项式队列中的最小元素就是某一个树的根节点，这样我们只要对所有的树依次扫描，花费O(log n)的时间复杂度，就能找到最小的元素

当我们需要往二项式队列里插入节点时，我们首先创建一个只有一个节点的树，接下来我们就按照rank增加的顺序，依次遍历所有的树。

在遍历的过程中，连接具有相同rank的树，直到我们找到了一个”空闲”的rank位置为止，相当于在对二进制数做进位运算。假如我们对一个大小为21的二项式队列插入一个节点，那么森林的组成会由原来的rank0, rank2, rank4，变成 rank1, rank2, rank4。这样做的话，最坏的情况是将节点插入到rank最大的树上，

在这种情况下，需要遍历k个树，同时连接k个树，对应的时间复杂度是 O(log n)

类似地，二进制加法就对应着两个二项式队列的合并，同理可得，所需要的时间复杂度也是 O(log n)

在这里面，最棘手的操作是删除二项式队列中最小的节点

我们首先在队列中删除根节点最小的树，但是却需要保留它的子节点，子节点本身需要做合并的操作。

以上操作需要的时间复杂度为O(log n)

对应的实现代码如下

trait Heap {
  type H // type of a heap
  type A // type of an element
  def ord: Ordering[A] // ordering on elements

  def empty: H // the empty heap
  def isEmpty(h: H): Boolean // whether the given heap h is empty

  def insert(x: A, h: H): H // the heap resulting from inserting x into h
  def meld(h1: H, h2: H): H // the heap resulting from merging h1 and h2

  def findMin(h: H): A // a minimum of the heap h
  def deleteMin(h: H): H // a heap resulting from deleting a minimum of h
}

trait BinomialHeap extends Heap {

  type Rank = Int
  case class Node(x: A, r: Rank, c: List[Node])
  override type H = List[Node]

  protected def root(t: Node) = t.x
  protected def rank(t: Node) = t.r
  
  // link 是一个辅助函数，用来处理两个相同rank的二叉树合并的过程
  // 为了在连接两个二叉树时维护堆有序的状态，我们将根较大的树设为根较小的树的子树。
  // 同时在子树中，由于插入了一个新的节点，rank值需要加1
  // 为了能高效地进行插入操作，这里
  protected def link(t1: Node, t2: Node): Node = // t1.r == t2.r
    if (ord.lteq(t1.x, t2.x)) Node(t1.x, t1.r + 1, t2 :: t1.c) else Node(t2.x, t2.r + 1, t1 :: t2.c)
  
  
  protected def ins(t: Node, ts: H): H = ts match {
    case Nil => List(t)
    case tp :: ts => // t.r <= tp.r
      if (t.r < tp.r) t :: tp :: ts else ins(link(t, tp), ts)
  }

  override def empty = Nil
  override def isEmpty(ts: H) = ts.isEmpty

  override def insert(x: A, ts: H) = ins(Node(x, 0, Nil), ts)
  override def meld(ts1: H, ts2: H) = (ts1, ts2) match {
    case (Nil, ts) => ts
    case (ts, Nil) => ts
    case (t1 :: ts1, t2 :: ts2) =>
      if (t1.r < t2.r) t1 :: meld(ts1, t2 :: ts2)
      else if (t2.r < t1.r) t2 :: meld(t1 :: ts1, ts2)
      else ins(link(t1, t2), meld(ts1, ts2))
  }

  override def findMin(ts: H) = ts match {
    case Nil => throw new NoSuchElementException("min of empty heap")
    case t :: Nil => root(t)
    case t :: ts =>
      val x = findMin(ts)
      if (ord.lteq(root(t), x)) root(t) else x
  }
  override def deleteMin(ts: H) = ts match {
    case Nil => throw new NoSuchElementException("delete min of empty heap")
    case t :: ts =>
      def getMin(t: Node, ts: H): (Node, H) = ts match {
        case Nil => (t, Nil)
        case tp :: tsp =>
          val (tq, tsq) = getMin(tp, tsp)
          if (ord.lteq(root(t), root(tq))) (t, ts) else (tq, t :: tsq)
      }
      val (Node(_, _, c), tsq) = getMin(t, ts)
      meld(c.reverse, tsq)
  }
}

回到正题

这里还会用到ScalaCheck来做测试

在代码中，有多个实现，只有一个是正确的，其他的都有Bug，你需要编写测试来测试出Bug。

这个作业非常贴心地给出了例子,教你如何写生成器

lazy val genMap: Gen[Map[Int,Int]] = oneOf(
  const(Map.empty[Int,Int]),
  for {
    k <- arbitrary[Int]
    v <- arbitrary[Int]
    m <- oneOf(const(Map.empty[Int,Int]), genMap)
  } yield m.updated(k, v)
)

• arbitrary[T] 是一个产生 T 类型数据的生成器，这里我们需要生成的是 Int 类型的 堆
• oneOf(gen1, gen2) 是一个随机的选择函数
• const(v) 是用来构造一个总是返回 v 的生成器

那么仿照着来写下

package quickcheck

import org.scalacheck._
import Arbitrary._
import Gen._
import Prop._

abstract class QuickCheckHeap extends Properties("Heap") with IntHeap {

  lazy val genHeap: Gen[H] = for {
    x <- arbitrary[Int]
    h <- oneOf(genHeap, const(empty))
  } yield insert(x, h)

  implicit lazy val arbHeap: Arbitrary[H] = Arbitrary(genHeap)

  property("findMin") = forAll { (h: H) =>
    val m = if (isEmpty(h)) 0 else findMin(h)
    findMin(insert(m, h)) == m
  }
}

这样编写的基础测试的通过率为 4/7

我们来看下这个测试的反向check

// in QucikCheckSuite

/** Turns a `Properties` instance into a single `Prop` by combining all the properties */
def asProp(properties: Properties): Prop =
  Prop.all(properties.properties.map(_._2).toSeq:_*)

def checkBogus(p: Properties): Unit = {
  def fail = throw new AssertionError(
    s"A bogus heap should NOT satisfy all properties. Try to find the bug!")

  check(asProp(p))(identity) match {
    case r: Result => r.status match {
      case _: Failed         => () // OK: scalacheck found a counter example!
      case p: PropException  => p.e match {
        case e: NoSuchElementException => () // OK: the implementation throws NSEE
        case _ => fail
      }
      case _ => fail
    }
  }
}


@Test def `Bogus (1) binomial heap does not satisfy properties. (10pts)`: Unit =
  checkBogus(new QuickCheckHeap with quickcheck.test.Bogus1BinomialHeap)


// in test/Heap.scala
trait Bogus1BinomialHeap extends BinomialHeap {
  override def findMin(ts: H) = ts match {
    case Nil => throw new NoSuchElementException("min of empty heap")
    case t :: ts => root(t)
  }
}

以上面这段为例

Bug的引入在于错误地实现了findMin函数

检查错误时，我们希望对于编写的测试，对有Bug的实现能找到反例，所以定义了一个辅助函数checkBogus

这个函数的行为和一般的测试相反，当匹配到反例或者NoSuchElementException时认为正确，其他情况认为是错误。

我们只要编写新的property来卡掉不正确的实现就行了

这里就要详细查看论文和对应数据结构的实现了，才能对症下药

我们可以看到，错误的实现改写的部分

trait Bogus1BinomialHeap extends BinomialHeap {
  override def findMin(ts: H) = ts match {
    case Nil => throw new NoSuchElementException("min of empty heap")
    case t :: ts => root(t)
  }
}

trait Bogus2BinomialHeap extends BinomialHeap {
  override protected def link(t1: Node, t2: Node): Node = // t1.r == t2.r
    if (!ord.lteq(t1.x, t2.x)) Node(t1.x, t1.r + 1, t2 :: t1.c) else Node(t2.x, t2.r + 1, t1 :: t2.c)
}

trait Bogus3BinomialHeap extends BinomialHeap {
  override protected def link(t1: Node, t2: Node): Node = // t1.r == t2.r
    if (ord.lteq(t1.x, t2.x)) Node(t1.x, t1.r + 1, t1 :: t1.c) else Node(t2.x, t2.r + 1, t2 :: t2.c)
}

trait Bogus4BinomialHeap extends BinomialHeap {
  override def deleteMin(ts: H) = ts match {
    case Nil => throw new NoSuchElementException("delete min of empty heap")
    case t :: ts => meld(t.c.reverse, ts)
  }
}

trait Bogus5BinomialHeap extends BinomialHeap {
  override def meld(ts1: H, ts2: H) = ts1 match {
    case Nil => ts2
    case t1 :: ts1 => List(Node(t1.x, t1.r, ts1 ++ ts2))
  }
}

编写测试有两种思路，一个是想出尽可能多且完备的测试来覆盖所有可能的情况

另一种就是针对性地构造hack测试，用尽可能少的测试分别暴露出每一个的问题

对于Bogus1BinomialHeap

trait Bogus1BinomialHeap extends BinomialHeap {
  override def findMin(ts: H) = ts match {
    case Nil => throw new NoSuchElementException("min of empty heap")
    case t :: ts => root(t)
  }
}

和正确的实现相比，他没有去ts部分寻找最小值

比如这个值，就会错

List(Node(0,0,List()), Node(-1,1,List(Node(-1,0,List()))))

我们写下的随机数据，插入一个最小值再返回就会出错

property("findMin") = forAll { (h: H) =>
  val m = if (isEmpty(h)) 0 else findMin(h)
  findMin(insert(m, h)) == m
}

同样的方法可以构造一些其他的测试，这里就不再赘述了。